Hubert Villuendas

Hubert Villuendas

PhD student in applied mathematics at the University of Grenoble Alpes, at the Jean Kuntzmann Laboratory and the Grenoble Computer Science Laboratory.

Posts by Collection

portfolio

Semidefinite Programming

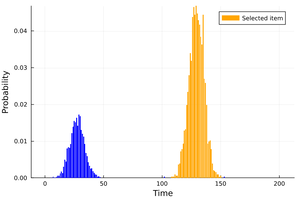
Dans le cadre de mon premier projet de thèse, j’ai étudié l’optimisation semidéfinie positive.

publications

Knapsack with compactness: a Semidefinite Approach

Published in Preprint arXiv, 2025

The min-knapsack problem with compactness constraints extends the classical knapsack problem, in the case of ordered items, by introducing a restriction ensuring that they cannot be too far apart. This problem has applications in statistics, particularly in the detection of change-points in time series. In this paper, we propose a semidefinite programming approach for this problem, incorporating compactness in constraints or in objective. We study and compare the different relaxations, and argue that our method provides high-quality heuristics and tight bounds. In particular, the single hyperparameter of our penalized semidefinite models naturally balances the trade-off between compactness and accuracy of the computed solutions. Numerical experiments illustrate, on the hardest instances, the effectiveness and versatility of our approach compared to the existing mixed-integer programming formulation.

Recommended citation: Hubert Villuendas, Mathieu Besançon and Jérôme Malick. (2024). "Knapsack with compactness: a semidefinite approach." preprint arXiv:2504.17543.
Download Paper

talks

teaching

Mathematics for Computer Science (TD)

M1 MoSIG, Université Grenoble Alpes, 2025

The aim of this course is to provide the necessary foundations for each student to be able to use the appropriate mathematical tools to develop well-founded reasoning and prove properties. It provides an overview of demonstration techniques, recurrence, bijections and algorithms, the basics of enumeration and combinatorics, divisibility, discrete structures and graphs, probabilities, modelling of classical laws, and random walks.

Probabilité et statistiques (TD)

L1, Université Grenoble Alpes, 2025

Premier semestre de l’année universitaire 2025-2026 : ce cours a pour but mettre en place les objets mathématiques primordiaux qui seront ensuite utilisés en statistiques, et intelligence artificielle. En particulier, ce cours introduit les notions de probabilités discrètes et continues, la loi des grands nombres et le théorème central limite.